QUIZZ Matematika Wajib (Kelas X)

JARIMATIKA: Perkalian cepat menggunakan jari tangan

1. Pengertian Jarimatika

Septi Peni Wulandari (2008: 2 ) Jarimatika adalah cara berhitung (operasi kalibagi- tambah-kurang) dengan menggunakan jari-jari tangan. Jarimatika adalah sebuah cara sederhana dan menyenangkan mengajarkan berhitung dasar kepada anak-anak menurut kaidah. Sedangkan menurut Dwi Sunar Prasetyono, dkk (2009: 19) “Jarimatika adalah suatu cara menghitung Matematika dengan menggunakan alat bantu jari”. 

Penggunaan alat bantu ini sejalan dengan penggunaan alat peraga agar konsep abstrak dalam matematika menjadi tampak kongkrit dengan adanya objek yang nyata. Untuk mempelajari konsep abstrak dalam matematika anak memerlukan objek atau kejadian konkret atau alat bantu pembelajaran (alat peraga) yang dapat berfungsi sebagai perantara atau proses visualisasi konsep. Tanpa menggunakan pendekatan-pendekatan tersebut, internalisasi konsep abstrak ke dalam pengetahuan kognitif anak akan sulit ditanamkan (Yumiati & Elang Krisnadi, 2008: 317).

Dari kedua pengertian di atas dapat dirumuskan bahwa jarimatika adalah suatu cara berhitung (operasi kali-bagi-tambah-kurang) dengan menggunakan alat bantu jari-jari tangan. Menurut (Wulandari, 2009) Kelebihan jarimatika sebagai media pembelajaran di antaranya adalah:

1) Jarimatika memberikan visualisasi proses berhitung.

2) Gerakan jari-jari tangan akan menarik minat anak.

3) Jarimatika relatif tidak memberatkan memori otak saat digunakan.

4) Alat yang digunakan tidak perlu dibeli.

2. Formasi Jarimatika Perkalian

Dalam perkembangan konsep matematika dengan menggunakan jarimatika, alat bantu yang digunakan dalam penelitian ini adalah jari tangan yang dimiliki siswa dan peneliti. Di bawah ini merupakan langkah-langkah pembelajaran perkalian kelompok dasar (bilangan 6-10):

1) Siswa terlebih dahulu perlu memahami angka atau lambang bilangan.

2) Siswa mengenali konsep operasi perkalian.

3) Siswa sebelumnya diajak bergembira, bisa dengan bernyanyi.

4) Mengenal lambang-lambang yang digunakan di dalam jarimatika. 

Perhatikan ilustasi formasi jarimatika berikut:

Gambar Formasi Jarimatika Perkalian 6-10

Sumber: Asri Wijiastuti dan Desiningsih (2013: 3)

3. Tahapan-tahapan mempelajari cara berhitung dengan menggunakan jarimatika

a) Siswa diajarkan cara-cara menghitung dengan jarimatika dengan ketentuan sebagai berikut: 

    Rumus: (T1 + T2) + (B1 x B2)

Keterangan: T1 = jari tangan kanan yang ditutup (puluhan)

                    T2 = jari tangan kiri yang ditutup (puluhan)

                    B1 = jari tangan kanan yang dibuka (satuan)

                    B2 = jari tangan kiri yang dibuka (satuan)

b) Guru dan siswa melakukan operasi perkalian dengan mendemonstrasikan menggunakan jari tangan.

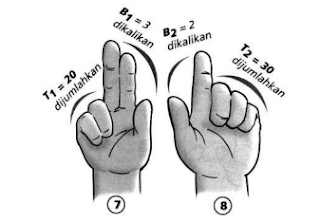
Gambar 3.Formasi Berhitung Perkalian

Sumber: Asri Wijiastuti dan Desiningsih (2013: 3)

Tangan kanan (7) : kelingking dan jari manis ditutup (dilipat).

Tangan kiri (8)     : kelingking, jari manis, dan jari tengah ditutup (dilipat).

7 x 8 dapat diselesaikan sebagai berikut.

Jari yang ditutup bernilai puluhan, dijumlahkan. Jari yang terbuka bernilai satuan, dikalikan. Formasi Jarimatikanya adalah sebagai berikut:

7 x 8 = (T1 + T2) + (B1 x B2)

         = (20 + 30) + (3 x 2)

         = 50 + 6

         = 56

c) Ajak siswa terus bergembira, jangan merepotkan anak untuk menghafal lambang-lambang jarimatika.

d) Melakukan latihan secara rutin dengan demikian anak merasa senang tanpa ada paksaan untuk menghafal.

VEKTOR (Matematika Peminatan Kelas X Semester Genap)

PENGERTIAN VEKTOR

Vektor adalah besaran yang mempunyai besar (nilai) dan arah.

Vektor digambarkan dengan sebuah Anak Panah.

Besar vektor dinyatakan dengan Panjang anak panah.

Arah vektor dinyatakan sebagai Arah anak panah (sudut yang dibentuk dengan sumbu X positif).

Vektor disajikan dalam bentuk ruas garis berarah

atau

ditulis vektor AB atau u       

A disebut titik  pangkal

B disebut titik  ujung

Notasi Penulisan Vektor
1. Bentuk vektor kolom:

2. Bentuk vektor baris:

3. Vektor ditulis dengan notasi i, j  dan k